Mastering PID Control: Techniques and Strategies for Tuning PID Parameters

Table of Contents

PID control (Proportional–Integral–Derivative control) is a classic algorithm widely used in industrial automation and process control. It is applied across numerous domains such as temperature, pressure, flow rate, and fluid level regulation. The core of PID control lies in precisely adjusting the system output by tuning the proportional (P), integral (I), and derivative (D) components. However, the effectiveness of a PID controller heavily depends on the tuning of its parameters—proportional gain (Kp), integral gain (Ki), and derivative gain (Kd). Proper selection and adjustment of these parameters are essential for achieving stable and efficient control performance.

Mastering PID Control: Techniques and Strategies for Tuning PID Parameters — **PID control**

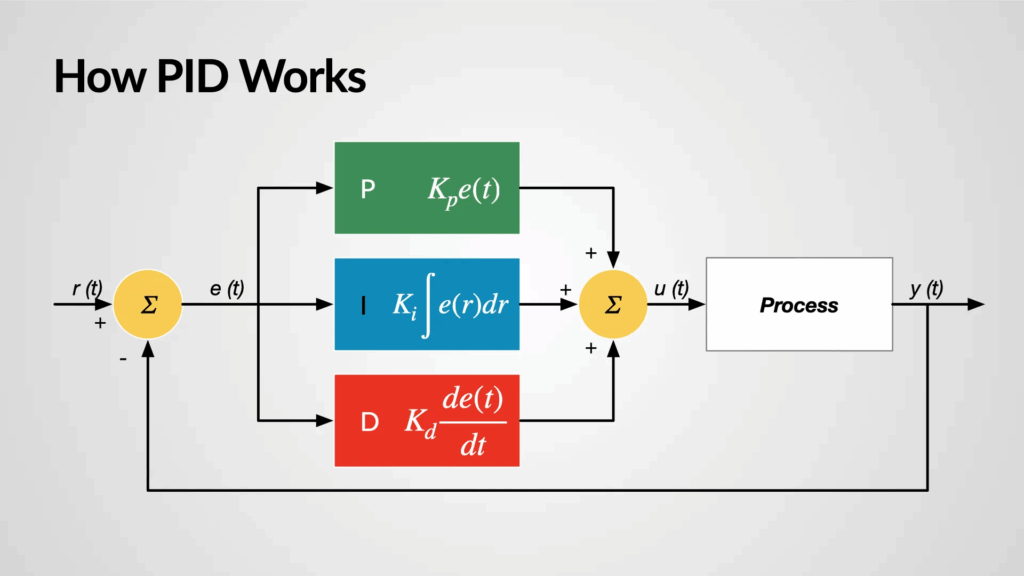
Challenges in PID Parameter Tuning

Tuning PID parameters is a highly technical task. It requires careful consideration of system dynamics, desired response characteristics, and control outcomes. Different application scenarios, equipment properties, and external disturbances all influence the choice of PID parameters. Although PID control is known for its simplicity and effectiveness, optimizing its performance in complex systems often demands iterative tuning and refinement.

PID Tuning Methods

1. Heuristic (Empirical) Tuning

Heuristic tuning is a traditional approach suitable for relatively simple and stable control systems. It relies on observing the system’s dynamic response and using predefined rules to estimate PID parameters. Common heuristic methods include:

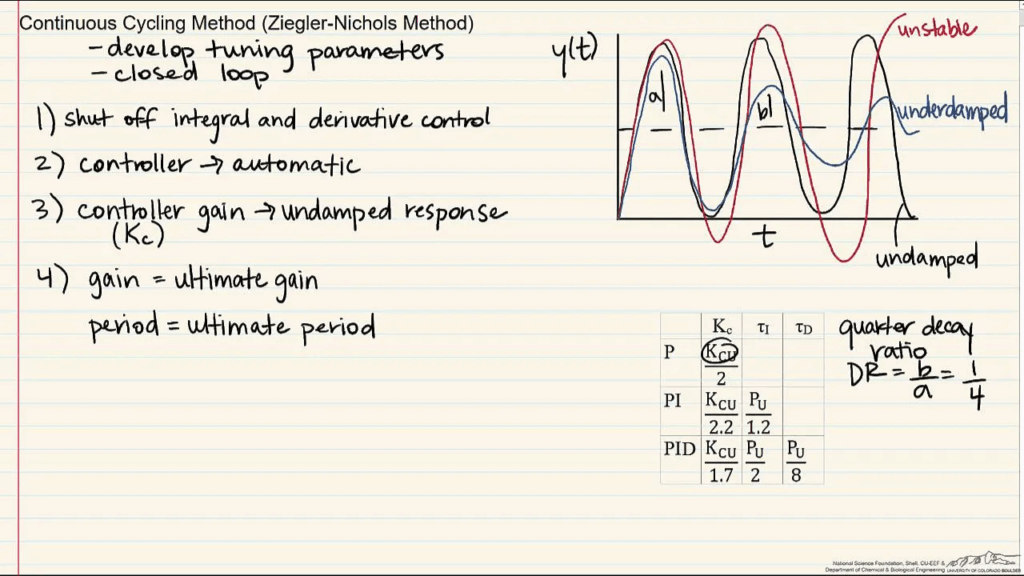
Ziegler-Nichols Method

One of the most widely used tuning techniques, the Ziegler-Nichols method involves the following steps:

Set the integral and derivative gains to zero, and increase the proportional gain until the system output shows sustained oscillations.
Record the proportional gain (Ku) and oscillation period (Pu).
Calculate the PID parameters using the following formulas:

Proportional gain:
Kp = 0.6 × Ku
Integral gain:
Ki = 2 × Kp / Pu
Derivative gain:
Kd = Kp × Pu / 8

This method offers a quick way to estimate initial PID parameters but may not provide optimal performance in complex or highly dynamic systems. In cases where system response is slow or lacks clear oscillation, Ziegler-Nichols tuning may not be feasible (Ziegler & Nichols, 1942).

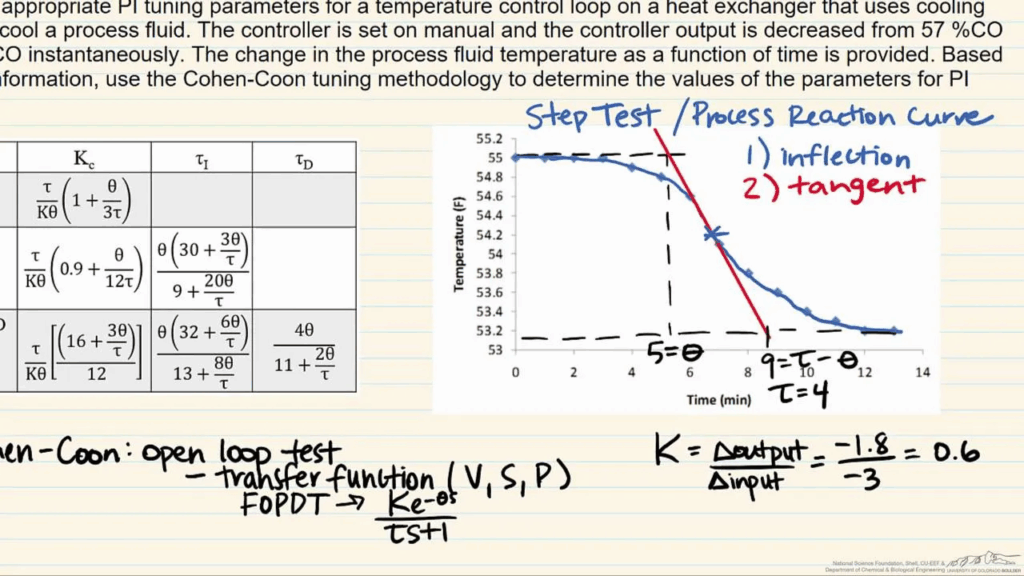
Cohen-Coon Method

The Cohen-Coon method is another empirical tuning technique, especially effective for systems with slow dynamics or noticeable time delays. Unlike Ziegler-Nichols, Cohen-Coon tuning better accommodates lagging system responses, making it a preferred choice in temperature or chemical process control (Cohen & Coon, 1953).

2. Trial-and-Error Tuning

The trial-and-error method involves manually adjusting PID parameters based on system feedback. Steps include:

Set initial values for PID parameters, either from estimation or heuristic methods.
Observe the system’s response to disturbances.
Incrementally adjust each parameter:
- Increase P gain to speed up the response.
- Adjust I gain to eliminate steady-state error.
- Fine-tune D gain to reduce overshoot and dampen oscillations.

This method is often used in practical settings where the controller is tuned in real-time. It requires experience and a clear understanding of system behavior for best results.

3. Optimization Algorithm-Based Tuning

With the advancement of computational capabilities, many modern PID controllers now employ optimization algorithms for parameter tuning. These methods use mathematical modeling and feedback data to find optimal PID settings.

Common Optimization Algorithms:

Genetic Algorithms (GA): Mimic natural selection to search for the best PID parameters. Effective for complex, nonlinear systems without precise models (Goldberg, 1989).
Particle Swarm Optimization (PSO): Inspired by the social behavior of birds or fish, PSO explores the parameter space to find optimal values. While generally fast and accurate, PSO can sometimes get trapped in local optima (Kennedy & Eberhart, 1995).
Fuzzy Logic Optimization: Combines fuzzy control principles with PID tuning. It is particularly useful for uncertain or nonlinear environments, offering greater robustness and adaptability (Zadeh, 1965).

These algorithms significantly enhance tuning efficiency and control accuracy. However, they require sufficient computational resources and detailed system models, which might limit their use in time-sensitive or resource-constrained applications.

Key Factors in PID Parameter Tuning

1. System Dynamics

Different control systems—linear, nonlinear, or time-varying—require different PID settings. Fast-responding systems may benefit from higher P and D gains, while sluggish systems may need stronger I action to eliminate steady-state errors. For nonlinear systems, advanced or adaptive PID strategies might be required.

2. Noise and Disturbances

In noisy environments, derivative control can amplify high-frequency signals, potentially destabilizing the system. To address this, D gain should be limited, and low-pass filters may be applied to smooth out the derivative term.

3. System Stability

Excessive PID gains can lead to instability and oscillation. A higher P gain improves response speed but may cause overshoot. Too much I gain can result in persistent oscillations. Tuning should balance speed, stability, and accuracy to ensure robust system behavior.

Real-World PID Tuning Example

Temperature Control System Case Study

Imagine using a PID controller to manage temperature in an industrial furnace. Initial PID settings are:

Kp = 1.0
Ki = 0.1
Kd = 0.05

Upon testing, the system heats quickly but overshoots the target temperature. The tuning process might include:

Reducing Kp to minimize overshoot and dampen oscillation.
Increasing Ki to eliminate steady-state error and ensure accurate final temperature.
Adjusting Kd to moderate temperature fluctuations during rapid changes.

Through iterative refinement, this method can achieve both responsive and stable temperature control.

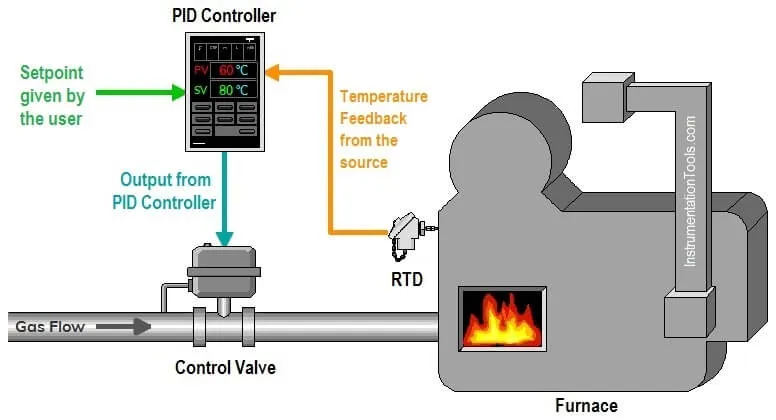
Conclusion PID Control

Tuning PID parameters is crucial for achieving precise and stable control in industrial systems. Whether using heuristic methods, trial-and-error, or advanced optimization algorithms, the tuning strategy should align with the system’s dynamics and practical constraints. While PID remains a reliable workhorse in automation, integrating it with adaptive or predictive control methods will further enhance its capabilities in modern, complex applications. PID Control

References

Cohen, H., & Coon, G. A. (1953). Theoretical considerations of retarded control. IEEE Transactions on Automatic Control, 2(1), 20-27. https://doi.org/10.1109/TAC.1957.1100047

Goldberg, D. E. (1989). Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wesley.

Kennedy, J., & Eberhart, R. C. (1995). Particle swarm optimization. Proceedings of the IEEE International Conference on Neural Networks, 4, 1942-1948. https://doi.org/10.1109/ICNN.1995.488968

Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8(3), 338-353. https://doi.org/10.1016/S0019-9958(65)90241-X

Ziegler, J. G., & Nichols, N. B. (1942). Optimum settings for automatic controllers. Transactions of the ASME, 64(11), 759–768. PID Control

Meta Description (for SEO):

Learn how to tune PID controllers effectively using heuristic methods, trial-and-error, and optimization algorithms. Boost control accuracy in temperature, pressure, flow, and level regulation.

If you’d like an HTML version or WordPress SEO plugin (e.g., RankMath) formatting, let me know.